미지수가 적을 때는 각 방정식을 정리하여 대입하여 해를 구하는 방법을 선택할 수 있겠지만, 미지수가 많을 경우 이러한 방법을 사용하여 해를 구하는 방법은 조금 무리가 있을 것이다. 미지수가 여러개인 연립 일차 방정식들이 주어졌을 때, 크래머 법칙(Cramer's rule, 혹은 크라메르 법칙)을 사용하면 비교적 간단하게 미지수들의 해를 구할 수가 있다.

(1)과 같은 식에서 A가 n×n인 정방행렬이며, 행렬식이 0이 아닌 비특이행렬이라고 하자. 이를 연립 방정식의 형태로 표현하자면 아래의 (2)와 같은 모양이 된다.

즉, (2)의 식을 행렬 A, B, x로 표현을 하면 (1)의 식과 같은 모양(b1, b2, ..., b3를 행렬B라 , a11, a12, ..., ann을 행렬A, x1, x2, ..., x3를 행렬x)이 되는 것이다. 이렇게 n까지 있는 연립 일차 방정식을 풀기 쉽게 계산하기 위해 행렬로 표현을 하도록 하자.
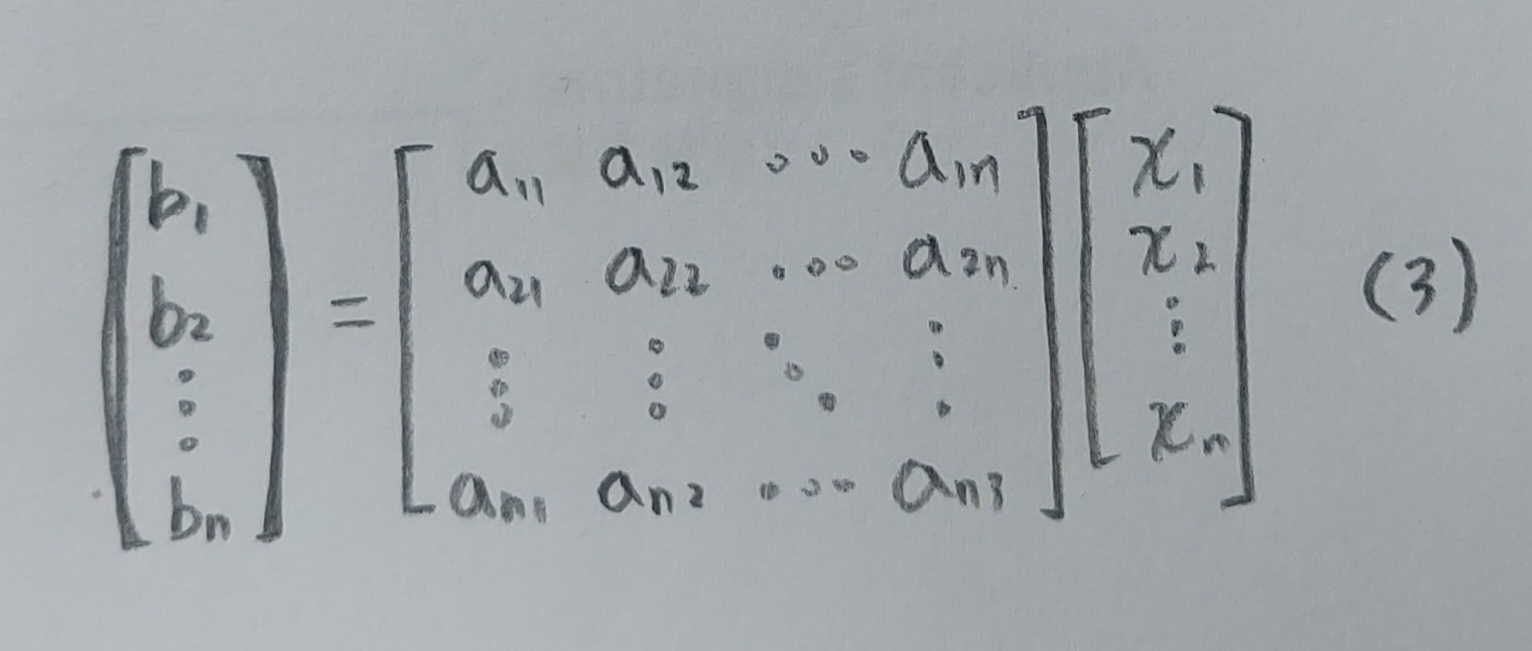
그러면 (3)과 같은 모양이 된다. 이러한 (2)와 (3)의 식을 토대로 우리는 A는 n×n인 정방행렬이며, x와 B는 n×1인 열벡터이라는 것을 확인할 수 있다.

이제 우리는 (1)의 식에서 A를 오른쪽으로 넘겨 계산을 하면 각 x를 구할 수가 있다. A행렬을 우변으로 넘기기 위해서는 A를 역행렬의 모양으로 넘겨줘야한다. A의 역행렬은 A의 부수행렬(adjoint, adj A)를 행렬식 │A│로 나누어주면 된다. 그러면 (4)와 같은 모양인데 이것이 Ax=B의 해가 되는 것이다. 이제 이 식을 풀어가면서 각x들의 해를 구해보도록 하자.

식 (4)를 풀어쓰면 식 (5)와 같은 모습이 된다. 먼저, │Cij│로 표시되는 여인자행렬과 행렬B를 곱해주자.

그러면 위와 같이 정리가 되는 것을 알 수 있다. ∑항들이 어렵게 보이겠지만, 라플라스전개의 식을 생각해보면 간단하게 이해할 수 있다. ∑bi│Ci1│은 행렬식│A│의 첫 번째 열을 열벡터 B로 대체하고 다른 모든 열을 그대로 둔 행렬식이 된다. 그리고 이를 │A1│이라고 하자. 그러면 당연히 하첨자가 2인 행렬식│A2│의 경우엔 두 번째 열을 열벡터 B로 대체한 행렬식, 하첨자가 3인 경우엔 세 번째 열을, 4라면 네 번째 열을 대체한 것이 되고, 이는 n번째도 마찬가지이다.

따라서, 식 (5)를 양변에 있는 서로 대응하는 원소들을 같게 놓으면 위와 같은 해를 얻을 수 있게 되는 것이다. 만약 하첨자 j가 2와 n 사이에 있다면 위와 같은 모양이 될 것이다.
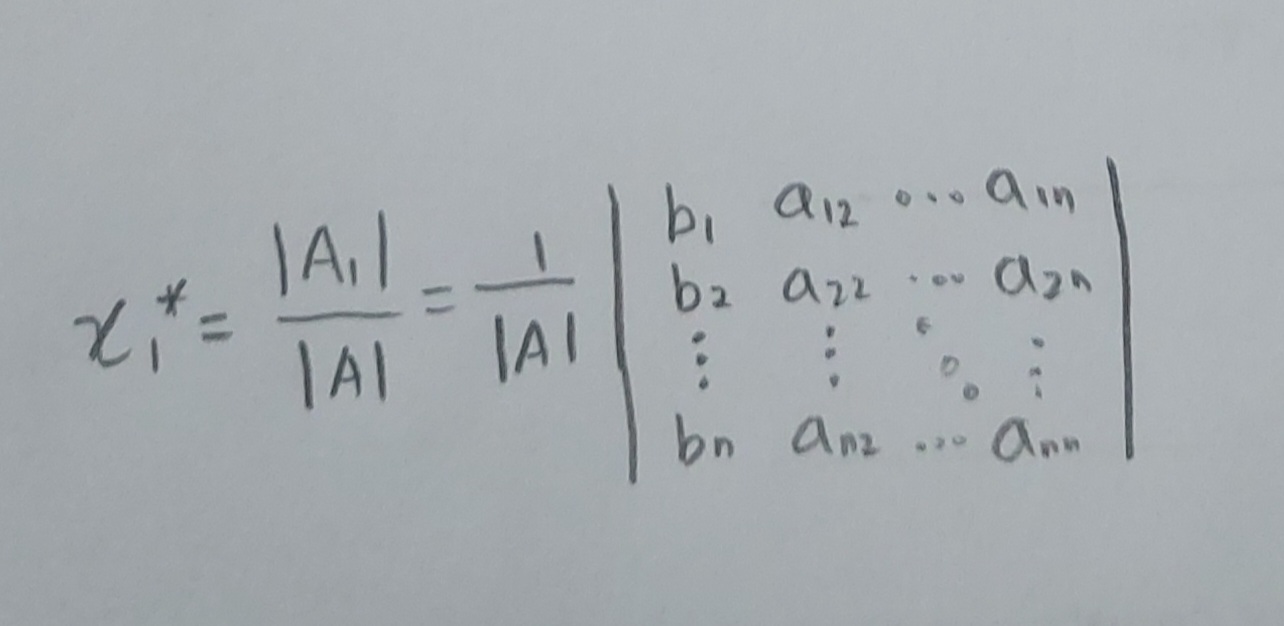
그렇기 때문에 역시 x1의 경우 위와 같은 식으로 간단히 구할 수가 있게 되는 것이다.
이렇게 단순히 보는 것보다는 예제를 풀어본다면 조금 더 쉽게 이해가 가능할 수 있을 것이다.

만약 위와 같이 3개의 방정식이 주어졌다고 하자. 먼저 이 식을 행렬로 나타내보면

이와 같은 모양으로 정리가 가능하다. 3×3인 정방행렬을 행렬A로 두자. 이제 우리는 행렬식│A│와 │A1│,│A2│,│A3│만 구하면 x1과 x2, x3의 해를 구할 수 있다.
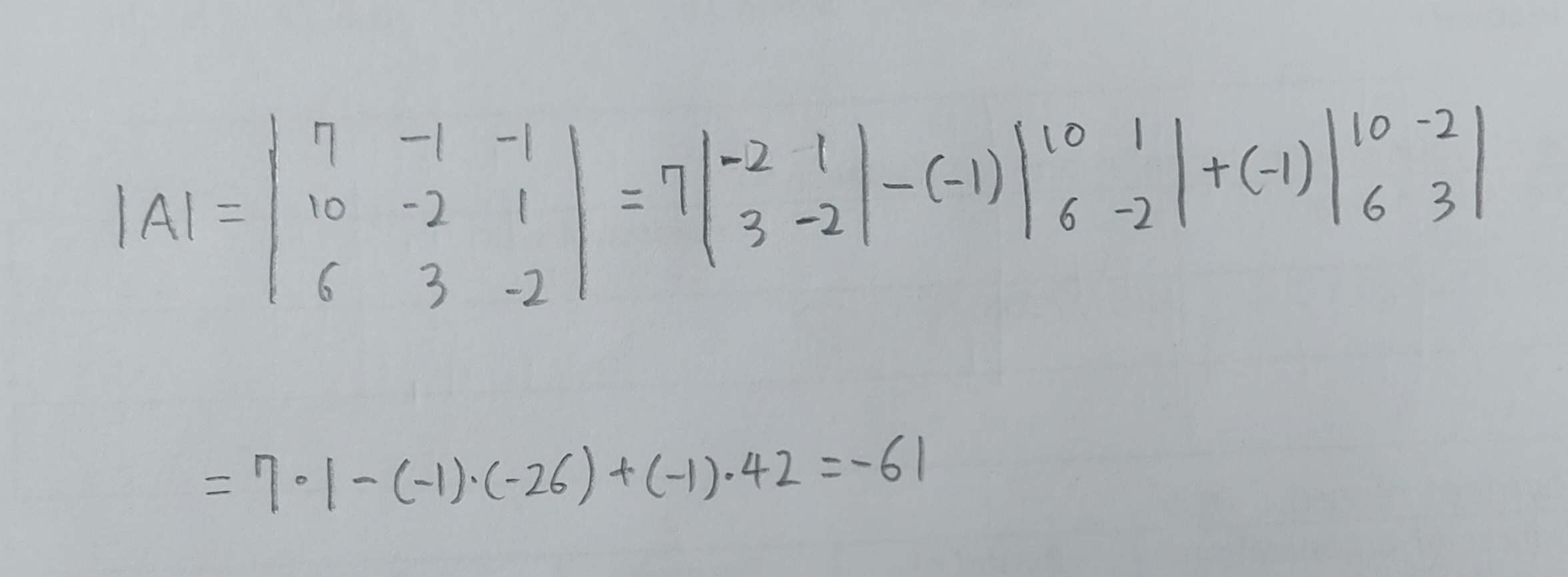
먼저 행렬식│A│를 구해보자. 라플라스전개방법을 통해 계산해보면 행렬식│A│는 -61이라는 값이 나오게 된다.
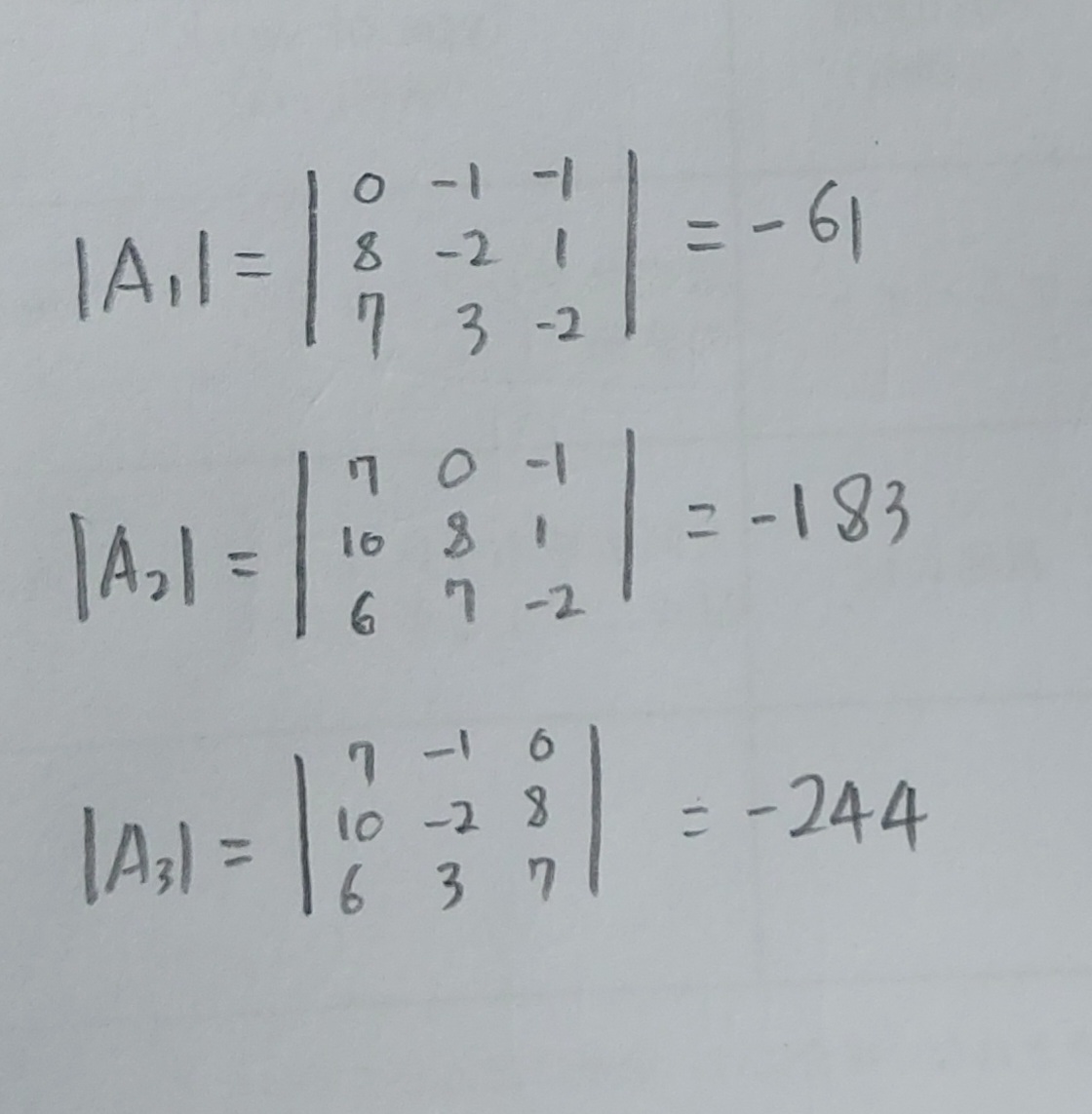
행렬식│A│를 구한 것과 마찬가지로 j=1,2,3을 모두 계산해보면 │A1│은 -61, │A2│는 -183, │A3│는 -244를 구할 수 있게 된다.
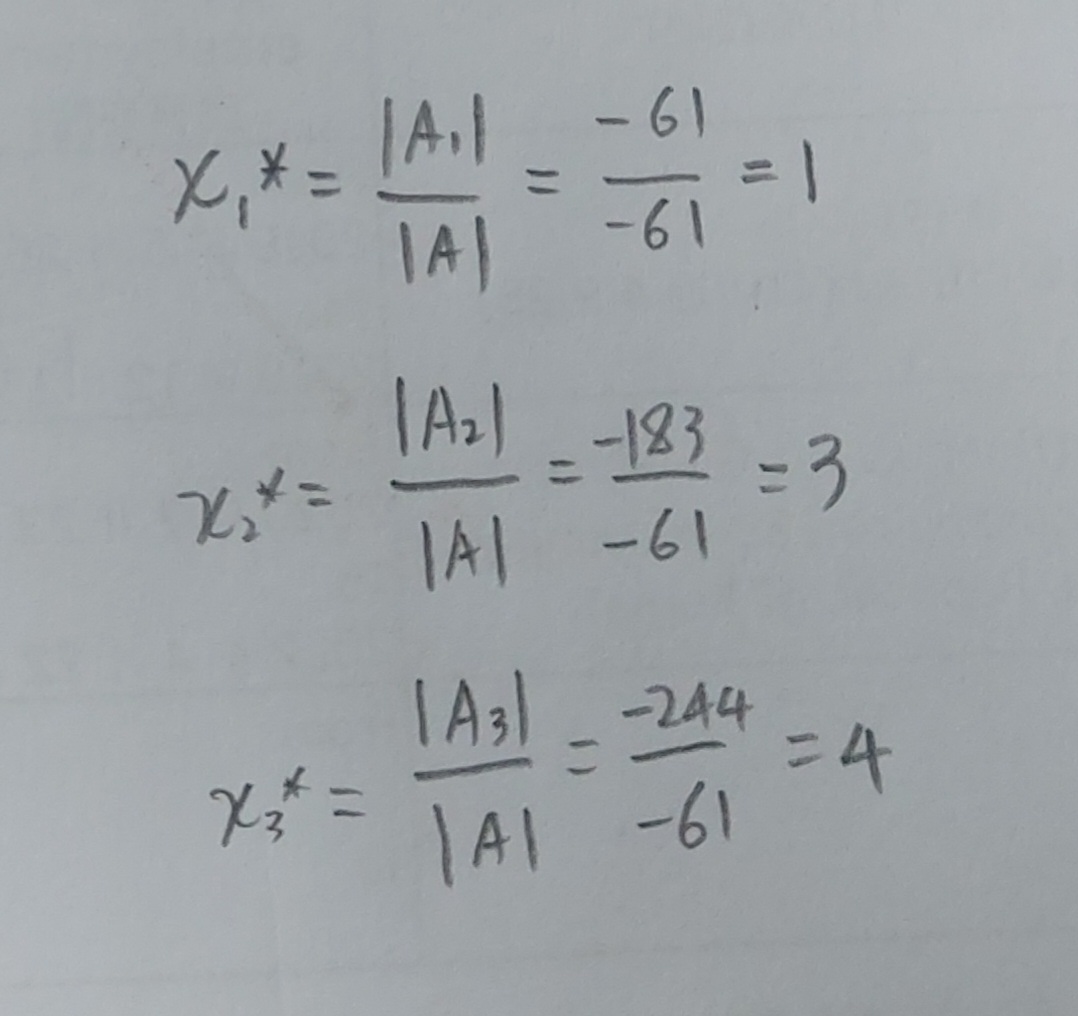
이제 │Aj│를 │A│로 나누어 주면 xj를 구할 수 있으니, 각각 계산을 해보면 x1은 1, x2는 3, x3는 4라는 해를 가진다는 것을 쉽게 찾을 수 있다.
'경제 갤러리 > 수학과 통계' 카테고리의 다른 글
| 라플라스 전개방법(Laplace expansion) - 고계행렬식 계산법 (0) | 2022.05.19 |
|---|---|
| 행렬식의 계산 (0) | 2021.11.20 |
| 근의 공식과 유리근 정리 (0) | 2021.10.10 |


